Lessons learned from Mohale
13 July 2007Palmi Johannesson and Sixtus L. Tohlang address the behaviour during and after reservoir filling of the 145m high Mohale CFRD in Lesotho, with emphasis on cracking of the concrete slab
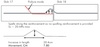
The 145m high Mohale CFRD was completed in 2000 in Lesotho. A background of the dam, including behaviour during construction, is addressed in References 1-4. In February 2006 heavy rains hit the Mohale region, resulting in a rapid rise of the reservoir to spilling conditions (Figure 1). This resulted in significant dam settlements downstream and cross valley movements of the crest, which in turn increased the already high compressive stresses within the center portion of the concrete slab, resulting in spalling failure of the slab.
The dam was visited on 13 February 2006, with no anomalies detected. The following day a crack in the concrete slab was reported. The slab cracking resulted in a significant jolt, which likely broke the bond between the concrete slab and the underlying extruded curb concrete. On 14 February 2006 at 02:24:58 hour the jolt was recorded on a micro-seismic station located on the left abutment, of seismic moment magnitude 1.2E+11 MNm. Freeing the slab from the curb concrete significantly reduced horizontal slab strain and increased the joint opening both for vertical as well as for perimeter joints at flank sections.
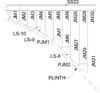
Figure 2 shows the maximum dam cross section with crest detail as well as zoning details close to the plinth perimeter joint. The dotted line indicates suggested modification of the outline of Zone 6, addressed in detail in Ref. 5. Figure 3 shows Mohale concrete slab, indicating the location of the main slab instrumentation. The location of the 14 February slab crack is indicated by a thick dotted line.
Assessment of instrumented behaviour indicates that the primary slab spalling that took place on 14 February was due to high horizontal strain between slabs 17 and 18 (Figures 4 and 5). Subsequently seepage increased significantly, peaking at some 600l/sec (Figure 6). As IWP&DC goes to press, an attempt is being made to determine the extent of slab cracking and the location of slab-leakage, by means of underwater cameras and divers.
Seepage assessment
If one assumes laminar flow through Zone 3, and that the zone of infiltration is sited at 100m depth one gets:
Q = 0.6m3/sec =A*(k*100/3.5); k =10-2 m/s: Inflow zone A=2.1m2.
If one assumes turbulent flow using Wilkins formula, with C=0.05 (Table 4-1 in Marulanda and Pinto, 2000) one gets:
Q=0.6m3/s=A*C*(100/3.5)0.54: A=1.96m2.
A relatively narrow crack in the slab may thus be feeding into Zone 3 area; at depth of ~100m, over an area of some 2m2.
Typical hydraulic settlement data vs head are plotted on Figure 7, showing rebound as the reservoir dropped. Based on measurements of the bent rebar shape taken on 5 March 2006 (see Figure 8) the horizontal overlapping amounted to 78mm. The apparent overlapping of the concrete joints may be as much as 120mm, while the right slab (#18) lifted up ~75mm above slab 17. The combined opening of vertical abutment joints amounts to some 340mm.
End of construction (EOC) deformations and modulus
Settlements during construction were measured at three dam cross sections. Details are provided in; a) the Mohale Dam Impoundment Manual, September 2002 and in; b) Appendix I to the Mohale Dam Design Report, Design Parameters, Stability Analyses and Static and Dynamic Deformation Analyses, March 2003; both prepared by the principal author of this paper as well as in References 5 and 6.
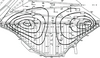
EOC iso-settlement lines for the maximum dam section are shown on Figure 9. EOC settlements for the three instrumented dam sections are listed in Table 1, yielding Mv (1D- modulus) for the u/s shell ~ 40 MPa and 30 MPa for the d/s shell, back-calculated from centerline settlement values (Poisson's ratio correction has not been done).
Within the dam cross section, the embankment settlement values used to assess Mv are affected by (internal) arching, i.e. d/s shell should settle more and u/s shell less if this arching (dragging down) was not in effect. The 2D modulus (considering the triangular dam shape) is probably closer to ~40* 0.8 = 32 MPa and that of the d/s shell around 30*0.8 = 24 MPa (detailed later in this paper). Shortcomings in empirical assessment may largely be overcome by careful 3D modelling.
The basalt is strong, however, very angular, with poor gradation and high void ratio. After initial compaction this fill takes on an interlocked - apparent modulus in the range of 100 MPa (Figure 10). However, once the load on top increases, grain breakage sets in, which may start at a vertical stress (Figure 10) of only 0.2 MPa.
With a better gradation, a modulus envelope as shown on Figure 10 may evolve, with grain breakage setting in first around 0.6-0.8 MPa, however, after collapsing of the initial grain structure, ending in a very low modulus. Similar experience has been gained from the Kárahnjúkar project, although constructed of fine graded basalt [5/6]. Analysis of published data on ita give a similar drop in modulus with increased vertical stress.
Measurements of surface movements and modulus during reservoir filling
The Mr (during impoundment) modulus is estimated by conventional method to ~70 MPa. Considering the rapid reduction in stress within the fill (see i.a. discussion on load cells), the Mr is probably closer to 60 MPa. This yields a ratio of Mr/Mv of 60/32 = 1.9. In view of 3D effects, one should expect the FLAC-2D analysis to over-estimate the horizontal deflection, which it does, but on Mohale not by much.
Figure 11-left shows the orientation of the principal stresses during construction, while Figure 11-right shows the rotated stresses once water load comes on.
For reservoir loading conditions close to the slab surface Penman and Charles (1985) suggested Poisson's ratio of zero. Saboya (1999) points out that Mr/Mv=(1-µr)/(1- µv); where µr and µv is the Poisson's ratio during reservoir filling and during construction, respectively. Inserting µr= 0 and µv= 0.3 and 0.25 yields Mr/Mv = 2.9 and 2.0 respectively. Giudici (2000) used µ of 0.26 in his 3D analyses of Tasmanian dams. For Tasmanian dams, Fitzpatrick (1885) reports on Mr/Mv in the range of 2, while this ratio for Mohale dam was 1.9 [5].
Stiffening of the Mohale dam crest was proposed during construction, in view of the significant grain breakage which took place as the dam embankment was raised (Figure 10). This suggestion was not followed with reference to precedent of other dams where such precautions had not been considered necessary as well as considering impact on schedule and cost. The experience with Mohale dam has demonstrated that site specific assessment, based on sound engineering principles, shall precede over robotic empirical design. Under this concept a vertical joint was provided in the Kárahnjúkar slab at El 498, much in line with the joint details of the New Exchequer and the Sigalda Intake dams [5], in addition to a bond breaker and 'space' between compression slabs.
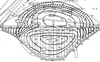
Figure 12 plots and Table 2 lists FLAC estimated as well as measured settlements of the embankment from EOC to September 2006. The FLAC contour lines (dotted) assume elastic behaviour while the measured contours include creep. Primarily for this reason, the settlements for measured values go deeper into the fill.
Figure 13 shows the measured settlement of the u/s slope, dam crest and the d/s slope of the Mohale dam. Previous experience shows that horizontal displacements are ~ 0.6* settlement of the crest, however, at Mohale the ratio is 140/400 = 0.35.
Figure 14 plots the FLAC slab deflection estimate for E 60 and 80 MPa, respectively, vs measured as of September 2006. The deflection of the concrete slab can be seen on Figure 15, taken for RWL 10m below the spillway crest, during natural lowering from spilling conditions.
Figures 16-18 plot cross valley and d/s movements as well as settlements of the dam surface due to water load, after cracking of the slab, with data up to September 2006.
Load cells within dam embankment
The Mohale load cells, as the instrumentation in general, have yielded excellent information. Data from the construction phase gave load in the outer shells about 15-20% above vertical gravity load measured from the sloped surface above, while the load in the center portion was around 0.8-0.9 times the gravity load, measured from the dam crest. This complies with FLAC simulation (Figure 11), comparing infinitely wide fill vs triangle dam shape fill. This is why Mv measured from dam center settlement data must be multiplied by 0.8-0.85 to get a true end-of-construction modulus (after correction; considered a 2D modulus). Once arching effect of steep valleys is considered this will further reduce the modulus, for Mohale probably to 50% of Mv.
Load cell reaction to the water pressure is plotted on Figure 19 vs time and on Figure 20 vs reservoir pressure in kPa; showing that the water load is not transferred onto the inner dam shell until substantial load has accrued (due to material strength and arching). However, at a certain point the load kicks in with almost the same gradient as the water load, see parallel lines on Figure 20. Figure 21 shows the loads in kPa over the dam cross section as measured by the load cells. Taking a section parallel to the dam surface at middle height, the pressure varies from 0.7 MPa at the surface to 0.385 MPa at the rock line. This results in Mr-modulus of 60 MPa.
Load cells on plinth back head
On Mohale a few load cells were placed on the back slope of the plinth where it became high (Figure 22). Readings from those cells are plotted on Figures 23-24. It is very interesting to note how the load on the heel of the plinth mobilises. Load does not follow conventional theory.
Limited load is transferred until plastic failure within the fill occurs at which time high load is transferred. This complies with the parallel lines of the internal load cells addressed above. This in turn means that stability of such retaining structures must be checked both for low load, with ko ~ 0.3 or less, but then also for ko approaching 1, in case of 'plastic failure' within the fill (small amount of sliding) as demonstrated on Figure 24.
Perimeter Joint Meters (PJM)
Locations of PJMs is shown on Figure 3. Max permanent joint openings of Mohale slab are listed in Table 3 and plotted on Figure 25 for PJM #4 and #9. Except for PJM 3 and 4, all movements have been plastic (permanent). Note the significant sudden jolt-movement of up to 30mm, occurring as the slab cracked on 14 February 2006. Combined JM-vertical joint opening and PJM movement in excess of 7cm, with shear as high as 4.6cm, is significant. This may have sheared some waterstops, in particular copper waterstops which are less flexible to shear movements than the rubber waterstops. Furthermore, the jolt, which went through the slab, probably caused instantaneous (cracking caused dynamic shock) movements in excess of permanent/recorded values.
Joint meter movements (JM)
Max openings of left abutment vertical joints located close to the crest are plotted on Figure 26 and listed in Table 4 with max value of 26mm.
JM openings on the left bank close to the plinth are listed in Table 5 and plotted vs time on Figure 27, while their location is shown schematically on Figure 28. Note that vertical joint openings are generally much larger close to the plinth than close to the crest.
Openings of the right bank JMs located close to the plinth are plotted vs time on Figure 30, with location shown schematically. Figure 31 plots the movement of those JMs, with X axis going parallel to the dam axis. Note the sudden joint opening as a result of the slab cracking. The sum of these vertical joint movements amounts to 169mm, while the sum of the left bank JMs opening amounts to 133mm, in total probably around 170mm, i.e. 340mm combined for both abutments.
Surface movements
Figures 32 to 34 plot Y (cross valley), X (d/s) movements and Z (settlement) movements vs time as surveyed from the Parapet wall and the d/s dam crest beacons. At lower elevations within the dam body, the collapsing effect seen by the settlement cell data during construction has already occurred to a significant degree, and the fill has come close to achieving elastic deformation modulus within the existing load range. For the u/s 30-40m and the dam crest this had not occurred, and accordingly, more significant plastic deformation occurred upon filling the reservoir for the fist time. Slab crushing induced movements amount to:
* Y: ~ 60mm in cross valley direction at middle flank sections, with total of 100mm
* X: ~ 130mm d/s movement of the max dam section at the crest, with total of 140mm
* Z: ~ 230mm settlement of the max dam section at the crest, with total of 400mm.
Figures35-37 plot the Y - cross valley movements, from left to the right abutment, the d/s (X) movements and settlements (Z), respectively. The dotted symmetry line on Figure 36 is drawn to underline the higher movement of the right flank. Mohale dam valley shape represents the left bank slope of 1: 2.3 and right bank slope of 1: 1.72. One would expect the steep right embankment fill constructed ahead of the left bank fill to deform less, due to a) higher portion of pre-impoundment settlement and b) greater 3D arching. Furthermore, the lack of symmetry noted from Figure 35 and Figure 36 is not seen in Figure 37. An explanation for this is not at hand.
Strains and stresses in slab
Strain variation vs time
Location of the strain cells placed in the Mohale dam is shown on Figure 3. These strain cells, having provided excellent data for back analysis, including where and when the failure(s) took place, if promptly interpreted, could have given warning of what was about to happen. Horizontal strains vs time in slabs 18 and 21 up-to and shortly after failure are plotted on Figure 38 and Figure 39, while the plot on Figure 40 shows vertical strain in slab 21.
Location and timing of slab cracking
Based on strain data from slab 18/21, slab cracking occurred first on 14 February at 2:24:58 hours, as also recorded by the local micro-seismic station, with cracking starting at the top at horizontal strain level of 590 micron, corresponding to compression of ~21 MPa (includes Poisson's correction). The water load at the top was inadequate to avoid lifting up and buckling of the slabs. A significant drop in horizontal strain was recorded at all strain-cells, in particular at cell 7B, Figure 41-left. This in turn increased vertical strain at depth (at El ~1976 masl), see plot on the right side on Figure 41. Vertical strain release (cracking) occurred at this level on 15 March at peak value of ~650 micron (´v = 0.00065), corresponding to compression of 19.5 MPa, without Poisson's ratio application, and ~24 MPa with Poisson's-ratio effect. A third stage cracking appears to have occurred on March 16. No significant vertical seepage increase was seen as result of this.
The strain data from slab 21, located four slabs to the right of the cracked slabs supports the above (Figure 42); with initial cracking at the top due to horizontal strain exceeding 600 micron around 14 February, with apparent later cracking at depth around 16 March due to vertical strain. This occurred one day after slab 17/18 cracked at depth i.e. the slab appears to have cracked in three phases, with possible 30-45° shear failure at El ~ 1976 left of slab 18 on 15 March and then a third phase shear cracking on 16 March at a higher level (say around 2020) right of slab 21.
Strain in slab vs elevation
Figure 43 plots the horizontal and vertical stresses in slab 21; a) at EOC; b) at the time of slab cracking and c) afterwards (by September 2006), at which time stresses had been greatly relieved as the bond broke between the slab and the extruded curb. The stresses are calculated by the following formula, applying Poisson's ratio of 0.25:
EQUATION HERE
Figure 44 plots adjusted horizontal, inclined and vertical stresses vs elevation in the concrete slab 18 and 21 at the time of failure. Means to avoid high horizontal strain in the slab are addressed later in this paper.
Relevant construction aspects of Mohale dam
Figure 45 shows the concrete beam at El 2040 carrying the paving equipment, which resulted in intensified compaction of the rockfill in this region. As the concrete beam and rails present a stiff foreign object just under the slab, in the authors view the reinforced concrete slab and steel rails should have been removed.
Figure 46 shows the u/s slope of the Mohale dam during initial reservoir filling. Note numerous cracks in the slab above joint 2040, with concentration in the region of the side ramp/later constructed fill, causing differential settlement after paving of the slab. Although surface reinforcement was added over the 2040 joint, its length above the vertical joint was inadequate. For this reason such reinforcement on Kárahnjúkar was made longer [6].
Figure 47 shows spalling at the slab/ plinth contact already occurring during construction, as the result of dam settlement, pushing the slab onto the plinth. While providing 'space' at this joint, e.g. by soft impregnated wood or similar, is helpful, reducing the downward movement of the slab by stiffer fill and other means addressed herein is most important.
Figure 48 shows tension/cross valley induced cracks which formed during construction in the curb concrete on the right bank. Note the already paved slab on the right side. Tension joints in the abutment are provided to cope with such movements, which cause compression in the center section of the slab. First at the Kárahnjúkar dam were lines of defense provided to handle such cross valley movements.
Figure 49 gives a view of the right bank of the Mohale dam during stage 1 construction, showing how badly the 1” shotcrete surface protection buckled due to massive settlement of the rockfill, while the extruded curb above did much better. For unknown reasons this shotcrete was not removed; see Figure 50.
Conclusions
Selection of rock for embankment fill, including rip-rap
Prior to involvement of the authora in the design of Mohale dam, it was planned to use only doleretic basalt for the embankment. This rock was found on the right reservoir flank under a thick cover of amygdaloidal basalt. Due to its hardness/ brittleness, doleretic basalt yields rockfill of high void ratio and high apparent modulus (after compaction). However, under increased vertical stress it undergoes massive grain breakage, resulting in an overall low modulus at 0.5-1 MPa vertical stress of only some 30-40 MPa (without 2D or 3D correction). It is believed that favouring doleretic basalt as embankment fill, or any such strong and brittle clean rock, is a 'left-over' from the outdated era specifying 'clean' rockfill. The weaker basalts tend to break up to a lesser skip gradation, with lower void ratio after compaction, thus providing fill with higher modulus.
Due to its brittle nature and high thermal conductivity doleretic basalt is not an ideal rock for rip-rap. Thermally induced tension from day-to-night cycles combined with very high modulus slices (tension cracking) the doleretic boulders to small fragments (Figure 51).
The authors feel that inadequate attention is placed on collecting in-situ performance data, which should be published in a CFRD-Performance-Catalogue, accessible to the profession at large. Laboratory tests are of value when correlated to such field performances. On Mohale, the pre-construction tests on different basalt rock types may have failed identifying resistance of 'dolerite' to cyclic weather exposure. Possibly other varieties of basalt may be equally or more durable under field exposure. The author is not aware of any field data or calibrated laboratory evidence indicating that amygdaloidal basalt is inferior to e.g. doleretic basalt for use in rip-rap or as concrete aggregate. We need to improve the testing methods, supported by field performance precedent, to arrive at a suitable characterization of rock for rip-rap and concrete aggregate. Some laboratory tests in use classify rock with 30-50 years excellent field performance as not suitable in concrete. In this field our knowledge needs to be advanced.
A somewhat different view on the durability of Lesotho basalts is presented in an excellent paper by Riemer (2003). There is probably need for a more in-depth assessment of the performance of rock, including amygdaloidal and doleritic Lesotho basalts, in the various zones of high CFRDs.
It is noted that quartzite, believed to have somewhat similar properties as doleritic basalt, was successfully used in the Cethana dam, yielding a very high modulus (Mv of 145 MPa). This simply demonstrates that if well executed, including carrying out proper quarry blasting tests, with the aim of producing uniform, low void ratio fill (~ 0.25), most rock can be used. Emphasis shall be placed on the u/s 30m zone and the crest section (H/4). A void ratio of 0.3-0.32 for the d/s shell is probably adequate in most cases. Except for the slab supporting zone (Zone 3), it appears more meaningful to specify void ratio and density rather than gradation.
Importance of watering the embankment
It is recommended that the u/s 30-40 m zone will be compacted at optimum moisture (Zone 3) or applying =200 l/m3 of water to the fill (Zone 4/5). Water shall also be used for the coarser rock, by keeping the rock wet at depth, helping grain breakage during construction. For budgetary purposes 100l/m3 is probably adequate.
Sequence of slab pouring
In the high portion of the dam the concrete slab should not be placed until the dam embankment has reached a level at least 0.75H.
Joints and strain in slab
Accumulated horizontal joint openings at Mohale from both abutments amounted to ~2*170mm=340mm, while overlapping of slabs 17/18 probably amounted to 120mm. This suggests that space between slabs in the compression zone should exceed say 220mm. Here 'space' means distance between concrete slabs, formed by impervious material, compressible to > 50% of its thickness at < 8 MPa. For dams of configuration similar to Mohale, constructed of low modulus embankment, the space between slabs at vertical joints should amount to four joints with 50mm gap at dam center, with some seven joints on either side of width 25mm. However, providing a stiffer embankment shall be given top priority.
In practice it is much more difficult to reduce the high vertical strain than the cross-valley induced horizontal strain. Remedial measures include a-c) high rockfill modulus, with emphasis on the u/s 30-40m section of the dam; d) providing space at the perimeter joint (~50mm, by soft wood or a similar low modulus sheet) and at all planned horizontal construction joints; e) placing the slab in the dam center portion as late as possible; f) providing viscous asphalt emulsion bond breaker between curb concrete and the slab in the compression zone (except at starter slabs), of thickness min 3-4mm; g) providing shear reinforcement at all planned joints; h) avoid thinning in the slab at all joints; i) place the main reinforcement 150mm from the surface; j) for slabs thicker than 0.6m, provide a second layer of reinforcement placed 100-150mm from the lower surface, of quantity 1/2 that of the surface layer [5/6].
For a slab paved in three phases, providing space at planned horizontal joints (including at the plinth perimeter joint) amounting to 3*50mm will for a 200m high dam with slope 1:1.3 reduce vertical strain in the slab approaching 3*0.050/(200x1.64) * 30000 = 13.7 MPa, say by 10 MPa. In most cases this would be adequate to avoid spalling at plinth and shear slab failure.
Parapet wall
Limit wall height to 6-6.5m and the length of each element to 7.5m (for flat abutments 15m may be used), with 'space' between elements of 25mm. When reservoir level rises frequently above the crest/slab joint level, at the slab/Parapet wall perimeter joint and at vertical Parapet wall joints, specify both copper and rubber waterstops.
Waterstops
At vertical abutment joints, provide both bottom copper waterstop as well as embedded rubber waterstop. At compression center slab vertical joints and at planned horizontal construction joints falling within 0.3H and 0.7H (measured from the river bed), provide bottom copper waterstop as well as either a short embedded rubber waterstop of a width of only 200mm, or provide a surface waterstop (copper, stainless steel or hypalon/PVC/HDPE) as a second line of defense (Reference 6, Figure 32). Along steep abutments and at high plinth sections, increase the height of the copper waterstop U to 100mm and provide a 150 mm wide stretching zone for the rubber waterstop [5/6]. As a 3rd line of defense along the perimeter joint, provide a hypalon waterstop (Reference 6, Figure 39).
List of symbols and abbreviations:
Abbreviations:
* CFRD and CFED: Concrete Faced Rockfill Dam and Concrete Faced Embankment Dam
* RWL: Retention water level, same as Full Supply Level
* RTE: Reservoir triggered earthquake, rather than reservoir induced earthquake
Symbols:
* E: Young's modulus, MPa
* Mv: One dimensional modulus of rockfill, in MPa
* Mr: Modulus used to estimate slab deflection during impoundment
* Poisons ratio; m = ´1/´2 = lateral expansion strain/axial compression strain.
P. Johannesson, President of Palmi Associates, USA: Email: palmi@palmiassociates.com; S. Tohlang, Chief Delegate, LHWC, Lesotho: Email tohlas@lhwc.org.ls
The authors are grateful to Landsvirkjun and the Kárahnjúkar Joint Venture, which includes Montgomery-Watson-Harza, in charge of the Kárahnjúkar dam design; and to Lesotho Highland Water Commission/ Lesotho Highland Water Authority; for the permission to use information from performance of Kárahnjúkar and Mohale CFRDs, respectively. Particular appreciation is expressed to Professor Dr. Kaare Hoeg and Dr. Wynfrith Riemer for valuable observations and editing comments, greatly enhancing this paper. Further appreciation is expressed to Bayardo Materon for his support and encouragement.
TablesTable 5 Table 1 Table 2 Table 3 Table 4