Waterhammer solutions
13 October 2006Small hydro plant designers often choose long penstocks instead of the traditional 'open channel' option, as they can be cheaper, quickly installed, and easier to maintain. However, these longer penstocks are usually affected by waterhammer phenomena, which must be faced with great care and suitable calculation models to verify in a reliable way that the stresses remain in a correct range – as was the case with one small hydro scheme in Italy
Gardone V.T. is a small hydro plant, the result of the rehabilitation and upgrade of a plant once owned by a military factory, where the head of seven other very small upstream plants, which were all decommissioned during the last 50 years, was concentrated. The water for Gardone V.T. originates from the river Mella, by means of a weir located in the north side of Gardone Val Trompia, a small industrial town in the province of Brescia, northern Italy. The drainage area is 241km2 with an average rainfall of 1.2mm per year.
Before the construction of the new plant, the water ran in a long canal, named Acqualunga, created specifically for it, crossing the whole town from north to south. Later, a secondary canal, called Gramineto, was built in the middle part. The existing plants were located on both the main canal and on the secondary ones, so some exploited the whole diverted water amount and some only a part of it. Nowadays, this partition has been removed and the whole flow rate runs in the new penstock.
The present maximum flow is 4.5m3/sec, corresponding to an average flow rate of about 3m3/sec (the maximum flow being increased slightly from 4m3/sec in order to guarantee the 3m3/sec average), but under a reserved flow obligation which is expected to increase dramatically in the future.
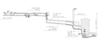
To exploit the whole head potential without any altimetric constraint, the existing open channels were substituted with a pressured pipe – a long penstock that carries the water from the first plant upstream to the last one downstream, saving the available head as pressure.
The optimum penstock diameter has been calculated as 1800mm, which allows an increase in the head exploitation of 6,64% thanks to the recover of the unexploited heads existing between every couple of contiguous plants. The main characteristics of the new plant in the final configuration are:
•Maximum flow rate: 4.5m3/sec.
•Average flow rate: 3m3/sec.
•Gross head: 27.3m.
•Nominal capacity: 803kW.
•Installed capacity: 1.3kVA.
•Annual production: 4MkWh.
The power plant and the tailrace, 360m long, will remain about the same as the last downstream plant.
As the length (>1.5km) of the depleted reach and the storage constant are significant, a relief discharge device was installed close to the plant to lower flow rate variations (emptying out and filling up) in the river caused by the unit start up and shut-down. Essentially, it is a Howell Bunger valve, installed under water, automatically driven by the control panel to maintain the flow rate in the penstock when the turbine is out of service.
Penstock characteristics
The first 202.8 m of the existing canal will remain unchanged; only a new trashrack and an automatic cleaner will be installed. In the following 321.1m, an underground reinforced concrete tunnel is now working in depressurised (approximately 1m of water) conditions to solve a mistake made during the construction: the bottom of the channel was rebuilt about 70cm higher than the old one, so only 20m3/sec can run in the open air channel. As the tunnel cannot be reshaped, nor can another one be excavated in the heart of the town, the study decided to create a depression column of about 1m, after having checked that the existing structures could tolerate the new external loads and having put a plastic coating to make it as air-proof as possible.
The water then begins to run underground in the 1.38m long penstock, which was made with three different technologies. The first 254.5m of penstock, under the national road of Val Trompia, consists of cast iron pipes, the following 768.4 m, which follow the borders of a new residential area, are glass reinforced pipes (GRP) and the last 357.1m, laying into the existing canals, is steel pipe coated with a reinforced concrete structure. Table 1 sums up the situation.
The first tests on the plant confirmed the good quality of the theoretical calculation, as the total reflection time was measured as 3.75 secs, corresponding to an average wave speed of 736m/sec, slightly lower than the calculation, possibly because of the lower actual value of the modulus of elasticity of GRP pipes and because of the smaller contribution of the coverage soil along this part of the penstock.
Waterhammer calculation
The waterhammer effects on the penstock have been investigated in two stages. First, the hydraulic functioning of the penstock and how the turbine and dissipation valve actions affect the pipes was calculated (by means of a simplified mathematical model); the calculations detected the more dangerous operations for the system and suggested the operating limitation of the unit to avoid overstress in the penstock. In a second stage, three sophisticated models were implemented to investigate the best solution to the waterhammer problems, (which turned out to be a surge tank) and to define its design parameters. Before the second model stage, a set of field tests was carried out to verify the hydraulic parameters of the penstock and the results of the theoretical calculations. At the end, another field tests campaign was carried out to set the operating parameters of the turbine and the dissipation valve, and to test the plant in the hardest working conditions.
Boundary conditions
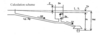
Penstock relevant data
•Static water level: 329.1m asl.
•Depressurised length: 321.1m.
•Penstock length: 1.380m.
•Penstock total length (depressurised + pressurised length): 1,701.1m.
•Hydraulic area of the pressurised penstock: 2.596m2.
•Theoretical average wave speed: 895m/sec.
•Theoretical reflection time: 3.8sec.
•Actual reflection time: 3.75sec.
•Actual wave speed: 736m/sec.
•Hydraulic losses coefficient: 0.1068sec2/m5.
Main turbine characteristics
•Type: Kaplan.
•Number of blades: five.
•Runner diameter: 950mm.
•Wicket gates axis level: 302.7m asl.
•Runner axis level: 302.33m asl.
•Geodetic head: 27.1m.
•Net head: 25.8m.
•Maximum flow rate: 4.5m3/sec.
•Rated power: 980kW.
•Rated speed: 750rpm.
•Maximum runway speed: 2,030rpm.
•Unit inertia (PD2): 5,258Nm2.
•Water contribution (PD2): 432Nm2.
•Total inertia (PD2): 5,690Nm2.
Hydraulic relevant transients
As a preliminary approach, the more dramatic situations for the
penstock stress are assumed to be:
•Overspeed caused by electric shut-off without wicket gates
closing (with the runner at stationary runaway condition).
•Electric shut off with wicket gates closing.
•Mechanical shut-off without over speed.
The preliminary simulations and the field tests are carried out under the abovementioned items.
Waterhammer stress minus surge tank
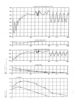
The preliminary calculations showed that significant overpressures (positive and negative) affect the penstock. So many field tests were carried out on the penstock in its original configuration (without surge tank) to validate the theoretical results and to define exactly the actual hydraulic working of the turbine/penstock system.
Phenomena connected with the negative pressures
The hydraulic and mechanical transients depend on the peculiar characteristics of the plant, which are:
•Very high hydraulic inertia, due to the penstock length.
•Very low mechanical inertia, due to the small value of the unit PD2.
The characteristic time of the mechanical inertia is about 0.9 secs, corresponding, when an electric shut-down occurs, to the acceleration rate of the unit running speed.
As the turbine is a Kaplan type, increasing the running speed corresponds to a similar increase of the flow rate, which causes a strong depression in the penstock. The maximum value is reached in case of overspeed due to runaway condition, but it changes only a little during the normal shut-down because of the long closing time of the wicket gates needed to limit the positive waterhammer pressure.
As the reflection time of the penstock is about 3.8 secs and the first increase of the flow rate comes in less than 1 sec, a direct waterhammer takes place in the penstock, so the first depression wave runs practically unchanged along the pipeline until 450m downstream of the siphoned channel, decreasing only in the last part. Nearby, the whole penstock is engaged by a transient of negative pressure, as reference to the atmospheric value, with a first maximum close to the absolute vacuum at the progressive 790, while the main part of the siphoned channel would be affected by the absolute vacuum.
In this situation, it would be necessary to install suitable devices to guarantee the air comes in, but the air bubbles in the penstock could arrive to the dissipation valve, causing a very strong waterhammer, with positive pressure waves of about 250m as a water column.
On the other side, without aeration valves, vacuum bubbles appear and they could implode under the ensuing positive pressure wave, causing very dangerous effects to the penstock. Referring to the positive overpressure, it occurs at every electric shut-down with correct closing actions of the wicket gates and runner blades. The calculation and the field tests show that the maximum pressure waves can be limited to standard values using a long closing time and suitable law for the wicket gates (a bilinear closing law is enough).
The main problem from the turbine operating transients is the negative pressure wave, which can’t be mitigated by external devices – such as the dissipation valve, which is very efficient for the positive pressure. Moreover, the dissipation valve must be operated under great care to avoid making the penstock situation worse. The only technical solution, which is consistently reliable, is a surge tank, installed in the penstock path between the power station and the progressive 790, where the vacuum problem becomes dramatic.
Waiting for the erection of the surge tank and taking into account the dangerous effects of the negative pressure of the transient waves, plant capacity was limited to 250kW, so as to operate in a safe condition in every situation.
Surge tank
Following the mathematical simulations and the morphology of the town where the penstock is located, the surge tank was erected at the progressive 1524.7m. This is quite close to the power station (145m upstream) so that a long part of the penstock can enjoy the benefits of the work. The surge tank, circular shaped, was built quite completely over the ground level, so it resembles a simple cilindric tower made of steel.
A short steel pipe 800mm in diameter connects the penstock to the surge tank, constituting the surge tank diaphragm. It has an hydraulic smoothed section, conic shaped (in order to have an asymmetric losses coefficient) at the top side, towards the tower; the idea was to get higher hydraulic losses for the water going into the surge tank and lower ones for the water coming out.
Thanks to its steel structure, the tower, which works as a surge tank, was erected in two weeks, during a scheduled out-of-service period of the plant for routine maintenance.
The main characteristics of the surge tank are:
•Internal diameter: 4m.
•Material: steel UNI EN 10025 S275 JR.
•Thickness: 11mm.
•Penstock axis level at the progressive 1524.7: 308.7m slm.
•Top of the tower: 336.6m slm.
•Tower net height from the ground: 23.6m.
Final situation
Thanks to the preliminary simulation and the field tests on the plant at limited capacity, a sophisticated mathematical model of the penstock was implemented to investigate the situation of the plant with a surge tank suitable to maintain the maximum stress in the penstock in the standard range. Because of the location of the plant in the town, the surge tank has the following two main constraints:
•Maximum diameter 4m, due to small available space.
•Reduction of the positive oscillation of water in the surge tank to limit the tower height.
The calculation scheme was resumed, then, where:
•Lg penstock length upstream of the surge tank: 1526.1m.
•Sg average penstock area: 2.596m2.
•Sv surge tank area: 12.566m2.
•SS’ diaphragm area: 0.503m2.
•Ksu hydraulic losses coefficient for the water going into the tank (m=0.7): 0.249sec2/m5.
•Kse hydraulic losses coefficient for the water coming out the tank (m=0.9): 0.412sec2/m5.
•L.S. static level of the water: 329.10m asl.
The preliminary simulation by simplified software finds the situations which cause the hardest stresses to the penstock, which are:
•Electric shut-down just at the end of the maximum positive load ramp: this is the worst condition for the negative pressure.
•Electric shut-down at maximum load when the flow rate in the penstock is at its maximum transient value: this is the worst condition for the positive pressure.
The simulation also supplies the law of the flow rate variation during the closing transient, which was used as an input for more sophisticated calculations.
The above conditions are used to simulate many different situations by means of three different software packages, to find out:
•The best closing law of wicket gates and runner.
•The diaphragm optimum size to fulfill the constraints.
Referring to the turbine closing law, the simulations suggest as a theoretical approach:
•Wicket gates: Quick closing time from 100% to 18% (corresponding to the braking start) – 50 secs, braking time from 18% to 0% – 30 secs.
•Runner blades: Linear closing time – 120 secs.
The calculations face the set of operating actions connected with the turbine opening till full load and the following shut-down as mentioned above, adopting a diaphragm with a diameter of 800mm, which the model said would be the smallest one to satisfy the design constraints. The calculation results show the pressure variation in the penstock section just upstream of the surge tank and at the progressive 790 as a very important issue also, corresponding to more critical vertex for the negative pressure; the small perturbation waves demonstrates that the surge tank creates a satisfying decoupling effect.
The maximum oscillation range of the water level in the surge tank has been verified by means of three different software tools, which confirmed the following values, which became the input data for the surge tank design:
•Minimum water level in the tower (negative wave): 320.85m asl.
•Maximum water level in the tower (positive wave): 335.6m asl.
•Elevation of the tower top: 336.6m asl.
•Freeboard over the maximum positive wave: 1m.
At end of the erection of the surge tank, a field survey was carried out to verify the actual situation of the penstock in the most dangerous situations. The tests allow a better definition of the turbine parameters, increasing the runner blades and wicket gates closing time in order to reduce the effects of the related waterhammer phenomena.
•Wicket gates: quick closing time from 100% to 12 % (corresponding to the braking start) – 165 secs, braking time from 12% to 0% – 140 secs.
•Runner blades: linear closing time - 250 secs.
The results of the tests show an excellent concordance with the theoretical calculations, so that every limitation to the plant which could start to work with the design flow rate could be removed.
Conclusion
In the particular situation at the Gardone V.T. plant, the calculations, and the adopted solutions are shown, where the most dangerous stresses come from the negative waterhammer pressures caused by the very quick increase of the flow rate (+30% on the rated flow in ~ 1 sec) when the Kaplan unit shuts down at full load. This event, if not completely analysed and faced in the designing phase, would cause an absolute vacuum in a part of the penstock, with possible severe damages to pipes and to nearby installations.
Author Info:
Paolo Cretti, Voith Siemens Hydro Power Generation, Fosse Ardeatine, 7/9 I-20092 Cinisello Balsamo (MI), Italy; and Nino Frosio, Studio Frosio, P. F. Calvi, 9 I-25125 Brescia, Italy. Emails: Paolo.Caretti@vs-hydro.com and nino.frosio@studiofrosio.it
This paper was orginally presented at the Hidroenergia ‘06 conference, organised by the British Hydropower Association and the European Small Hydropower Association
TablesTable 1