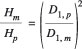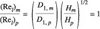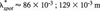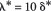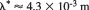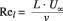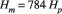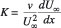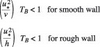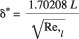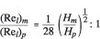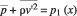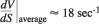Challenges to turbine development
12 July 2007The 14 Francis turbine units installed in the left power house at China's Three Gorges project were all commissioned successfully during the period June 2003 to September 2005, functioning as expected. However, all these turbines have developed a pattern of damage mainly on the guide-vanes which has never before been reported. Here S C Li, S H Liu and Y L Wu provide a brief description of damage observations, together with analysis of possible causes
The turbines developed for China's Three Gorges project are some of the world largest Francis turbines in terms of their capacity (710MW) and geometric dimensions (9800mm of runner diameter). The 14 units installed in the left power house were all successfully commissioned from June 2003 to September 2005, generating electricity normally. The machines were supplied by two consortiums - alstom/HEC, and GE/voith-siemens/DFEM [29].
On 14 October 2005 damage was spotted on No 11 turbine ('11F' will be used in the article, following the abbreviation employed at the Three Gorges Power Station) which had operated for 10,245.78 hours. This damage was examined and the guide plate was repaired. Similar damages were however found on 10F on 27 December 2005 (operated 11924.55 hours), on 9F on 11 December 2005 (2328.41 hours) and in the rest of the units (e.g. 5F and 6F etc).
The significance of the Three Gorges project itself is obvious in terms of technology development and economic-social-environmental effects. Furthermore 12 similar turbines are being installed in the right power house with an additional six machines needed in the underground power house. Other hydro projects employing turbines of similar scale are also being developed by China Yangtze Three Gorge Project Development Cooperation (CTGPC). For example, 18 turbines of 770MW capacity each will be utilised at the Xiluodu Project with eight 750MW turbines needed for Xiangjiaba. In addition, 18x825MW units for Baihetan project and 10 units of 700MW capacity each for Wudongde project are at the feasibility study stage, totalling about 90 turbines. Development of a further 1000MW hydro capacity is under consideration. Under such a strategy for hydro power development, these damages, although their impact on the machine operation is insignificant1, has been brought to the attention of CTGPC management, and needs to be thoroughly investigated.
Questions that immediately arise are: (1) Is this a new phenomenon associated with extremely large turbines?; (2) Should new technologies be sought and developed to combat this problem? As a result a meeting was called at the Three Gorges site from 12-14 March 2006, attended by research engineers, university academics and manufacturer representatives. A few days later (19 March 2006), the first author was invited to inspect the damage (Figure 1) on the 11F unit, in particular the damage on the representative No 4 guide vane. This article is mainly based on the in-situ inspection.
In response to such a challenge, a research centre has been set up in the State Key Laboratory of Hydroscience and Engineering, Tsinghua University, Beijing, where follow-up studies are being performed by a specially assembled team consisting of the authors and other Chinese colleagues from Tsinghua Universities and the CTGPC. The outcome will benefit not only the power industry but also our scientific knowledge in general.
The power house is shown by the model (Figure 2), and the specifications of the 11F turbine are as follows:
* Rated power 710MW
* Max efficiency guaranteed 96.26%
* Rated head 80.6m
* Min head 61m
* Max head 113m
* Rated speed 75 rpm
* Run away speed <150 rpm
For the majority of the time, unit 11F has been operating under low head conditions (around and below 70m).
Damage observed
The damage observed on the No 4 guide vane of 11F turbine is representative. The guide vane is a positively curved hydrofoil as shown in Figure 3. The turbine has 24 guide vanes and 24 stay vanes (Figure 4).
Damages occur only on the foil's lower surface in the form of horizontal strips, starting from the favourable pressure gradient (FPG) zone extending into adverse pressure gradient (APG) zone as shown by Figure 5. The depth of damage area is much less than the 1mm fully covered by corroded rough surface as shown by Figure 8. Heated tail on the damaged surface is observed (Figures 6, 7 and the red-circled area in Figure 8), which is another common feature. These damage strips lie approximately in the direction of free-stream flow. Another feature is the wedged head which almost always presents2 (Figure 9). The damage strips are distributed span-wise, showing regularities (Figure 5), with average span-wise spacing.
Analysis and considerations
Such damages on guide vane have not been reported before and it puzzles professionals. It has been proposed that among all possibilities, cavitation (damage) needs to be considered first despite the fact that the damage appearance as well as location did not comply with conventional cavitation damages often observed on Francis turbines [20 and 21]. The following analyses and considerations based on both metallurgical and fluid dynamic sciences strongly suggest a new type of cavitation (erosion).
Metallurgical considerations
Heated tail
The observed heated (blue and other) colour zone at the tails of damaged areas indicates a temperature range of 250°C-600°C (termed as 'bluing' in heat-treatment3) is encountered. The only hydrodynamic mechanism involved in a Francis turbine capable of generating temperatures at or above this range is cavitation. The experimentally proven temperature that a collapsing single bubble could generate is about 6000°C-7000°C4. One may argue: 'why is the damage compared with those often observed in Francis turbines, in particular those made of low-alloy steels before 1980's, very different'. Typical cavitation damage is featured by sponge-like deep erosion, such as shown in Figure 10. Nowadays, materials with better cavitation resistance are used such as the martensitic stainless steel (containing 13% Cr and 4% Ni or 17% Cr and 7% Ni) replacing low-Mn steel for fabricating machines. The material used for 11F is X3CrNiMo13-4 (EN-1088), which is close or equivalent to CA6MN (12.9% Cr, 4% Ni and 0.04% C), a commonly used martensitic stainless steel for turbine fabrications [18]. The striking force (i.e. cavitation attack) in this case is relatively weak owing to both the high overall pressure in the guide vane passage5 and the mechanism of this particular cavitation6. The heated zone itself is such an evidence that a relatively weak cavitation attacks relatively high cavitation-resistant material. Why? Heating effect always presents during cavitation attack, but if damage rate is high, the heated portion of material is removed immediately and simultaneously by bubble strikes. Therefore, we cannot see the heated zone afterwards. The heated part of the material may remain visible only if cavitation erosion rate is low. The very low erosion rate (much less than 1mm over 10,000 hours) in this case is consistent with this hypothesis.
Corrosion appearance
The appearance and feel of the shallow damaged area has led some experts to conclude that corrosion is the underlying cause responsible for the damage [eg. 20]. However, corrosion is only a consequence of cavitation damage and the following analysis may help to clarify this.
This material is a martensitic stainless steel as suggested by its brand. For austenite stainless steels, sensitisation is a well-known phenomenon of heat effect that causes inter-granular corrosion and is a widespread problem. The stainless character of stainless steels occurs when the concentration of chromium exceeds about 12 wt%. When an austenite stainless steel is exposed to a temperature range between 620°C to 676°C, subject to exposure-time as well as its own composition, the carbon will diffuse towards grain boundaries where the high concentration of carbon ties up chromium by forming chromium carbidesat grain boundaries, which leaves a zone of chromium depletion (below 12%) in the immediate area around the grain boundary, making this area less corrosion resistant than the bulk material and resulting in inter-granular corrosion. Such typical corrosion (on 304) is shown in Figure 11. The mechanism of sensitisation is conceptually shown by Figure 12. Recent studies found that sensitisation causing inter-granular corrosion is also a potential problem for martensitic stainless steels because it is a Fe-Cr-C system and is always used in the tempered condition7 in which carbides are precipitated. Investigations [eg. 2] show a trend that the maximum susceptibility to inter-granular corrosion was observed in the condition tempered at 500°C to 550°C, and a sensitized structure was detected. For lower tempering temperatures, it was less sensitized, or not at all, and for higher tempering temperatures, it was also less sensitized. A typical case (UNS S41000) is shown in Figure 13 (550°C), and the characteristic value variations with temperature (for two hours) is shown in Figure 14. A zone of high sensitization-susceptibility is indicated clearly for temperatures ranging from 500°C to 600°C.
According to the above understanding, the blue colour (plus other spectra of colors) on the heated tail of the damaged area strongly suggests a similar heat treatment at the temperature range of 500°C to 600°C that creates an ideal environment for sensitization, leading to inter-granular corrosion. This explains the metallurgical reasons for corrosion to appear on the damaged area of this martensitic stainless steel after cavitation attack.
Fluid dynamics consideration
The damage pattern does not suggest a large structure of cavitating flow that directly strikes and causes the damage, whereas the wedged head of damage strips gives a hint: are there any links with turbulent spots generated during boundary layer transition to turbulence that is also featured by wedge head?
Based on inspection in situ, it has been suggested that this new type of cavitation is related to the boundary layers streaks and presumably induced by turbulent production during the transition process [20 & 21]. This can be explained by examining the conditions required to enable nuclei in boundary layers to grow (cavitate) and how the boundary-layer can provide such conditions through its transition process8.
Cavitation inception
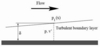
Many studies, as summarized in [19], show that cavitation inception is closely related with and strongly influenced by boundary layer transition. For boundary shear layer, the statistical properties of bubbles are dominated by the pressure-fluctuation field in terms of intensity and duration. Therefore, distribution of the turbulence level, which varies across the boundary layer, alters the statistical characteristics of micro-bubble inception performance across the boundary layer. This phenomenon was firstly demonstrated by Daily & Johnson [5]. The lowest mean pressure across the boundary layer is the location where the turbulence level is highest, since (Figure 15):

where p1(x) is the pressure in the free flow region beyond the boundary layer where V'2 is negligible; and p is mean pressure.
It is obvious that bubbles at this particular location have the highest probability to cavitate owing to the minimum value of mean pressure and the maximum value of instant pressure drop. The influences of magnitude and time scale of turbulence on cavitation inception were also demonstrated by many other studies on inception scale effect. For example, as early as 1981 Arakari & Acosta [4] emphasied the importance of time scale of turbulence supported by experiment observations. The frequency of the most unstable Tollmien-Schlichting wave in the laminar boundary layer just prior to transition is about 5 kHz, equal to a reference time period of 0.2msec for growth, which is about the same order as the bubble life-time (0.1msec) observed in their experiments. Huang [11] also found that the inception is correlated with the spatial amplification ratio through the mechanism of laminar to turbulent transition or laminar separation. Based on Kolmogorov theory for homogeneous and isotropic turbulence, for fully developed boundary layer flow, Arndt & George [6] suggested that if

the nuclei in the flow will have enough time to respond to the entire spectrum of turbulence. Otherwise only a fraction below the frequency of TB is sensed by the micro-bubbles9.
Therefore, for nuclei to cavitate, long enough negative pressure drop generated in the boundary-layer is essential, for which the turbulence production during boundary-layer transition provides such an opportunity. Therefore, we need to investigate how the laminar boundary layer in our case can break down and produce such turbulence for nuclei to grow.
Free stream turbulence and boundary layer transition
The difficulty is that the origin of turbulent flow and transition from laminar to turbulent flow still remains an unsolved challenge for fluid mechanics despite decades of study. Currently, even for flows over a flat plate, no mathematical model can precisely predict the transition Reynolds number because of a variety of influences, such as free-stream turbulence and surface roughness. Owing to the availability of linear stability methods and the knowledge of breakdown mechanism being initial condition dependent, most studies aim at understanding the source of initial disturbances rather than the details of the later stages of transition [25]. However the discovery of the Soliton-like Coherent Structure (SCS) by Lee [14 and 15] gives a much clearer picture of the low-speed streak formation and its breakdown, which helps to clarify the complex burst phenomena. There are two different kinds of flow structures which have been referred as stream-wise vortices by other researchers. One is the real stream-wise vortex. The other is the long streak containing several SCS, often referred to as solitary quasi-stream-wise vortex10. A long streak containing several SCS appears in the very near-wall region. The middle layer has two real stream-wise vortices which are the relatively long quasi-stream-wise vortices (often counter-rotating pairs). The interaction between the secondary closed vortex and the [SYMBOL HERE]-vortex produces the chain of ring vortices (i.e. high frequency vortices), leading to breakdown and turbulent production. Figure 16 shows the evolutions from SCS to a long streak and its breakdown.
For turbines, owing to complexities in geometry and off-design operation, much less is known [24]. For hydro turbines, the interplay of boundary layer transition with cavitation inception is important but little study has been done. Despite these difficulties, it is still possible to understand the phenomenon based on the knowledge gained from flat plate cases.
For 3D boundary-layer flows over (hydro) foil, cross-flow instability may dominate the breakdown while T-S waves act as generators of fundamental low-frequency secondary modes, but are neither important for their growth nor for breakdown [30]. For the current problem, the damage pattern on the guide vane suggests that it is virtually a 2D flow. The resulting perturbed flows are span-wise-dependent but essentially unidirectional, i.e. the transverse velocity components are much smaller than the stream-wise component. The instability of such transversely sheared flows appears to be related to various aspects of the transition process, such as secondary instabilities and by-pass transition. Many factors [33] can cause three-dimensional steady and unsteady distortions in the form of stream-wise or longitudinal vortices. These include small steady or unsteady perturbations11 superimposed on the oncoming flow, imperfections at the leading edge12, cross-flow instability, and Görtler vortices induced by surface curvature, as well as certain excitation devices13. Distortion of this kind also arises due to the nonlinear interaction between pairs of Tollmien-Schlichting waves.
Free-stream turbulence initiates three distinct motions within the boundary layer, as summarised by Saric et al [25]. The first motion is a sustained, streaky (z ' 2d), high amplitude (?u'? ' 5 - 10%U`) motion, which is probably due to stretching of the ingested free-stream vorticity and the growth of transient modes, i.e. the Klebanoff mode. The second is an outer-layer oscillation at T-S frequencies that grows weakly in the stream direction. The third is the usual T-S mode, which exhibits higher growth rates.
Currently we only have limited understanding about the instability of Klabenoff mode and its role in the transition owing to the random nature of both the free-stream disturbances and the Klebanoff motion. Most studies so far investigate steady distortions, induced in a controlled manner through the receptivity at leading edge only14. The maximum growth of this K-mode distortion is a function of Reynolds number and wave number, e.g. as demonstrated by Anderson et al [3]. In Figure 17(a), b is span-wise wave number,

Where b* is the dimensional span-wise wave number and b is the non-dimensional span-wise wave number valued as b = 0.45 for maximum transient growth. The mechanism of the downstream response to upstream disturbance is visualised by Figure 17(b). The calculated initial disturbance at x0= 0 is outside the boundary layer, while its downstream response is inside the boundary layer. Thus, this numerical simulation demonstrates well the receptivity at the leading edge: the disturbances at the leading edge that cause the largest growth of stream-wise streaks inside the boundary layer are vortices aligned in the stream-wise direction outside the boundary layer.
The free-stream turbulence poses an important influence on cavitation inception in boundary layer by altering boundary-layer instabilities (e.g. the growth of K-mode etc) through receptivity mechanism. This has been shown by Gates & Acosta in 1979 [10] that free-stream turbulence is an important factor for inception scaling; and that the mechanism through which this factor influences inception is the structural alteration of the boundary layer in terms of its separation and/or transition15. This is crucial particularly for extremely large turbines, the difference of Reynolds number (based on main flow parameter, reflecting the status of free-stream turbulence) between model and prototype is in the order of 102, reflecting a significant difference on turbulence level16 and consequently its influence on cavitation inception in boundary-layer. Therefore, the K-mode involvement (responding to the free-stream turbulence) in our case should be further considered.
Firstly, the guide plate increased free-stream turbulence is a primary concern in the sense of receptivity and the transient growth of K-mode instability, which may bypass the primary OSE17 mode and lead to early and random breakdown and turbulent production, although the flow in the first half of guide-vane passage is a highly accelerating flow18, i.e. with strong favourable pressure gradient, which would have a prolonged laminar boundary layer until transition if the level of free-stream turbulence was low.
Secondary, the wedged head of damage strips highly resembles the turbulent spots caused by such a streak (K-mode) transient growth and breakdown in a Blasius boundary-layer, which leads to a turbulent wedge. As an example, the work by Watmuff [31] demonstrates the evolution of a turbulent wedge from stream-wise streak. The final stages of growth and the ultimate breakdown of the streak are shown in Figure 18(a-c). The breakdown on the centre-line and the formation of two regions of highly unsteady flow on either side of the streak are most clearly evident in the contours of the broadband unsteadiness shown in Figure 18(c). It is evident that streak is responsible for introducing a new pair of streaks on either side via some instability mechanism, causing span-wise growth of the wedge since a span-wise succession of new streaks is observed in the early stages of its development. Here U + uf is the total phase averaged stream-wise velocity; u' is the background (broadband) unsteadiness; and u'' is the phase averaged unsteadiness. The wedge-shaped turbulent spot can also be visualised by using both shear sensitive liquid crystal (SSLC) and temperature sensitive liquid crystals (TSLC). The results [8] show the dependency of wedge spreading angle on the level of flow acceleration, referring to Figure 19 and Table 1.
Lastly, as demonstrated experimentally by Matsubara et al. (2000) [23], the growth of near-wall streaks is a key phenomenon triggering the bypass transition leading to breakdown and turbulent production. The mechanism of breakdown postulated by Lee [14 & 15] suggests that the generation of the high frequency vortices, i.e. the chain of ring vortices results from the interaction of the secondly closed vortex with the L-vortex. For our case, these vortices will surely create a favourable environment for nuclei to grow.
Discussion
The above considerations led the authors to think that in the case of particularly large turbines the scale effect19 means that the turbulent production occurs in the area where flow is most susceptive to cavitation inception20. Indeed, initial results from ongoing numerical simulation reveals such trends - a detailed report on this will be provided in the near future.
Model-prototype similarity
Free stream turbulence
It is always the case that the free-stream turbulence level of prototype is much higher than that of the model turbine, which makes the prototype, in particular for large turbines, more susceptible to the formation of low-speed streak and the transitional breakdown through the receptivity mechanism. In case of Three Gorges' turbines, if the similarity of free stream turbulence were required, by assuming a prototype-model scale of 28, the Reynolds number equality would have required

that is,

In reality, this is impossible owing to the constraints of the test rig leading to a much smaller Reynolds number for model tests. For Three Gorge turbines, the prototype's Reynolds number is approximately Re,p ' 4.6 x 107 at Qopt = 718m3/sec, while for models, it might be 102:103 smaller21. This implies that the free-stream turbulence level is much higher for the prototype.
For the turbines in the left power house, the flow in the guide-vane passages is further subject to a high level of free-stream turbulence. A guide plate in the spiral case prior to the entrance of the stay-vane passage (Figure 20) produces a high level of low-frequency disturbance which penetrates most into the boundary layer through receptivity mechanism. Obviously, the designer intended to reduce the unit size by employing this guide plate. However, the premature damage of the guide plate (a piece torn off) and subsequent severe pressure-fluctuation and machine-vibration are all evidence of high free-stream turbulence. Research has shown that span-wise distortions (modulations) can be induced by various free-stream disturbances. For example, small low-frequency three-dimensional perturbations in the free stream can produce significant distortion within the boundary layer, leading to alternating span-wise thickening and thinning [9]. Steady disturbances (e.g. artificial roughness, vortices etc) can also cause a similar type of span-wise modulation [e.g. 7]. And these distortions are all in the form of elongated streaks named as Klebanoff mode or K-mode as mentioned earlier [12, 32 and 13].
Boundary layer similarity
Boundary-layer similarity not only requires similar free-stream conditions but also an equality of boundary-layer based Reynolds number,

Owing to the equality of Strouhal number (i.e.n1'), this leads to

That is, for our case (i.e. the prototype-model ratio of 28), the boundary-layer similarity requires

In reality, as mentioned before, it is impossible to use such a high head for model tests. This constraint makes the ratio of two boundary layer based Reynolds numbers far away from unity, in the range of

Therefore, there is absolutely no boundary-layer similarity for model and prototype, making the prototype much more susceptible to turbulent transition.
This means that if no cavitation is observed during model tests it does not guarantee the Three Gorges turbines will remain free from cavitation inception in the boundary layer and subsequent erosion.
Estimation of laminar streaks and turbulent spots
Finally, we need to examine if the span-wise spacing of the damage strips complies with the span-wise distribution of K-mode streak breakdown and turbulence production in order to conclude our analysis.
The span-wise wave-length (spacing) of laminar streaks or Klebanoff wave l*, can be estimated22 as

Here, d* is the displacement thickness,

From a typical damage strip observed, say L = 0.550m, we have Re,l = 5.2x106 (based on U`'12.4m/sec) and d* = 0.43x10-3m. This gives a span-wise wave length

The transition region is characterised by a random appearance of turbulent spots. Assuming a spot generated from 20-30 such streaks, the turbulent spot spacing l*spot will be

It is approximately equivalent to the observed strip spacing l*strip ('0.100m). Surprisingly, the characteristics of K-mode streak breakdown and turbulent-production are all supportive of the hypothesis that the cavitation inception is triggered by the streak breakdown and turbulent production in boundary-layer. Thus, a dynamic process follows: once the first cavitation damaged spot is created, it will serve well as a roughness spot for triggering cavitation inception and create another cavitation damaged area immediately downstream. This dynamic process progresses stream-wise, resulting in such a horizontal damage strip with a wedged head and heated tail. These span-wise distributed stream-wise damage strips thus become dominant patterns on the guide vane.
Remarks
Although a full investigation is still underway, this article produced from the in situ inspection report provides a brief description of this new type of cavitation together with supportive evidence about its causes which has never been reported before.
The analysis shows that this is a new challenge for the development of large turbines owing to the violation of similarity law in the sense of both free-stream turbulence and boundary layer turbulence. To combat this problem, fundamental research together with the development of novel design and manufacture concepts should be carried out as a priority.
Table 1 Figure 1: S C Li (right) inspecting the turbines in the left power house together with the Deputy Director of Mech. & Elec. Division of CTGPC, Prof Dai Jiang Figure 1 Figure 2: Cross section of the Three Gorges plant model (Courtesy Harbin Electric Works) Figure 2 Figure 3: No 4 guide vane Figure 3 Figure 4: Plan view of 11F turbine Figure 4 Figure 5: Damages on the lower surface on all guide vanes showing nearly the same pattern Figure 5 Figure 6: Heated sign on the top surface between guide vanes Figure 6 Figure 7: Heated tail on the guide vane Figure 7 Figure 8: Damaged surface Figure 8 Figure 9: A representative damage-strip showing wedged head Figure 9 Figure 10: Typical sponge-like erosion pattern caused by a leading edge caviation attack (4000 hour operation) Figure 10 Figure 11: Grain decohesion due to inter-granular corrosion [26] Figure 11 Figure 12: Conceptual sketch of sensitisation, a) chromium depleted zone susceptible to inter-granular corrosion, b) chromium distribution across the grain boundary [28] Figure 12 Figure 13: OPtical micrographs of UNS S41000 steel specimens after oxalic acod etch test: tempered at 550°C Figure 13 Figure 14: Comparison among electrochemical tests to discriminate degrees of sensitisation for different tempering temperatures. Characteristic values are ir/ia for the DL-EPR, imin for the potentiostatic test, and i2max/icrit and Q2max/icrit for the potFigure 14 Figure 15: Conceptual sketch of (turbulent) boundary layer Figure 15 Figure 16: (a) T-S wave and CSS. The hydrogen bubble wire was at x = 250mm and y = 0.75mm; (b) The _-vortex structure. The wire was positioned at x = 300mm and y = 0.75mm; (c) Development of the _-vortex and the long streak. The wire was at x = 350mm and Figure 16 Figure 17: (a) Contour plot of maximum transient growth vs. ? and Reynolds number. The dashed line describes ? for which the maximum transient growth occurs given a specific Reynolds number. Here x0 = 0 [3]. (b) a) Velocity vectors in the z - y plane ofFigure 17 Figure 18: True spatial contours in plane, y = 2mm (a) (U +u?)/U1. (b) ????. (c) broadband unsteadiness, ???? [31] Figure 18 Figure 19: SSLC results for the turbulent wedge under sero, mild and strong (favourite) pressure gradients respectively [8] Figure 19 Figure 20: Guide plate (circled) shown on the model of the turbine Figure 20 (1) (2) (3) (3a) (4) (5) (6) (7) (8) (9) (10) (11) (12) (13) (14) Author Info:
S C Li, Fluid Dynamics Research Centre, Warwick University, Coventry, UK. Email: S.Li@warwick.ac.uk
S H Liu and Y L Wu, State Key Lab of Hydroscience and Engineering, Tsinghua University, Beijing, 100084, China.
The authors would like to express sincere thanks to the EPSRC's Warwick-IMRC for long term financial support (R.ESCM.9001 and R.ESCM9004) on turbine technology and cavitation and to CTGPC for its financial and technical support during the first authors visit to the Three Gorges Station from 19-20 March 2006. Thanks also go to Prof Dai Jiang, the Deputy Director of Mechanical & Electrical Division of CTGPC, Prof Lee C B, State key laboratory for turbulence research and complex system, Peking University and Professor K Sen, the Indian Institute of Technology, New Delhi, for valuable discussions.
TablesTable 1